QUIZ 2

pdf download  video w/o sound

Hardy Weinberg -MOVIE

Having now fully understood (?) all the major types of variations from "normal" Mendedlian type genetic patterns of inheritance does our newly found insight into Mendelian genetics have any impact upon our appreciation of evolution?

Remember, while "....populations evolve and individuals do not", the gene pool of a population is the summation of all the individual genomes within that population.

To rephrase the question, therefore, How might an understanding of Mendelian genetics (which addresses phenotypic expression of an individual's genes) allow us to understand phenotypic/genetic changes within a population?

Genetic Variation within Populations

To recap (in light of the last few lectures):

For a population to evolve, its members must possess variation, which is the raw material on which "agents" or "forces" of evolution act (genetic variation within a gene pool).

    

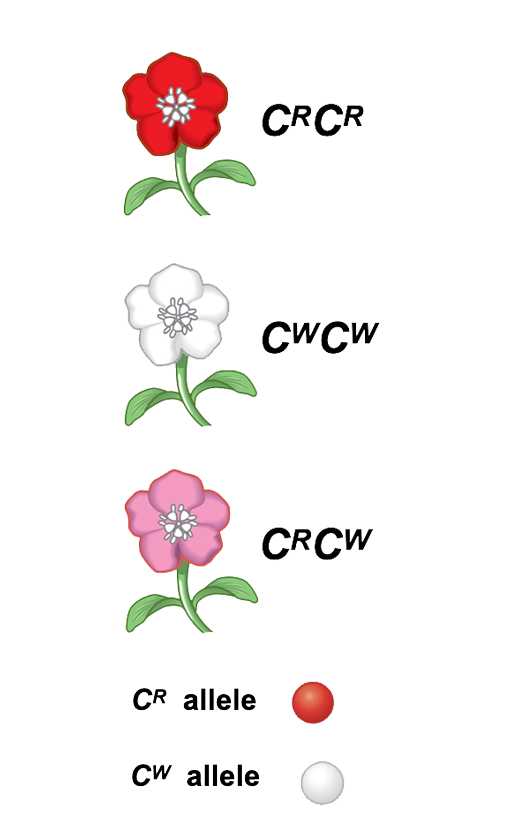
We observe phenotypes in nature: i.e. the physical expressions of genes.

A heritable trait, however, is a genetic characteristic of an organism that is mainly influenced by the organism's genes (we cannot forget totally the influence of environment on this expression).

The genetic component that governs a given trait is called its genotype.
A population evolves when individuals with different genotypes survive or reproduce at different rates.

Genes have different forms called alleles.

A single individual has only some of the alleles found in a population.

The sum of all the alleles in a population is its gene pool, which contains the variation (different alleles) that produce the differing phenotypes, upon which change can come about...evolution.

Most populations are genetically variable.

Natural populations possess inherent genetic variation.

The reproductive contribution of a genotype or phenotype to subsequent generations relative to the contribution of other genotypes or phenotypes in the same population is called fitness.

This "fitness" of any particular genotype is determined by the average rates of survival and reproduction of individuals within that population with that particular genotype;

i.e. the relative reproductuctive contribution of a given genotype.

For example, Man's highly selective preferences for certain edible crops have placed a a selective pressure on the crops that have been and are produced, giving rise to a seemingly wide variety ofimportant crop plants.

Artificial selection in laboratories that have analyzed genetic variation in assorted laboratory organisms, such as Drosophila melanogaster have also revealed genetic variation in these fruit flies.

In Ecological terms a locally interbreeding group within a geographic population is called a Mendelian population.

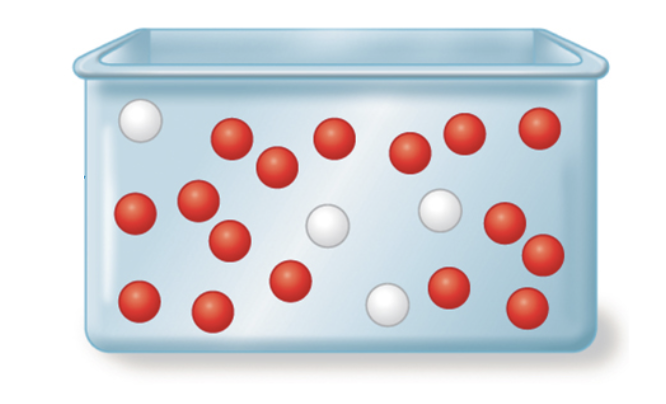
The relative proportions, or frequencies, of all alleles in this population are a measure of its population's genetic variation.

Population Geneticists can estimate such allele frequencies for any given locus by measuring the numbers of alleles in a sample of individuals from within a population.

Such measurements can be seen in terms of probability, which can range from 0 to 1, wherein the 

Sum of all allele frequencies at any given gene at any given gene locus = 1.

Thus, the allelic frequency, can be expressed in probabilities for any given trait,  which can be calculated by dividing the number of copies of that particular allele in a population by the sum of alleles in the population.

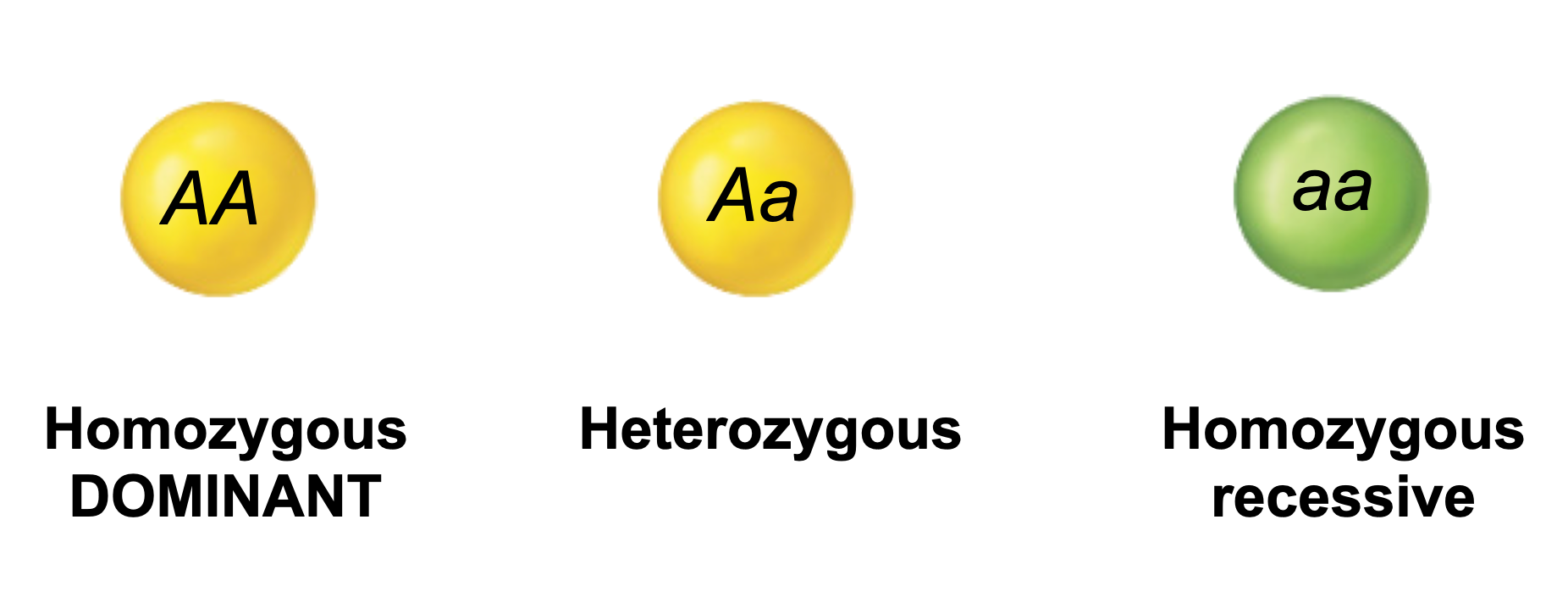
According to Mendelian genetics; If only two alleles (A and a) are present for a given locus, and both these alleles are found among the members of a diploid population, they may combine to form three different genotypes: AA, Aa, and aa.

Thus:

The Allelic frequency can be calculated using simple mathematics with the following variables:

n AA = the number of individuals that are homozygous for the A allele (AA).

n Aa = the number of individuals that are heterozygous (Aa).

n aa = the number of individuals that are homozygous for the a allele (aa).

Note that n AA + n Aa + n aa must always = N, the total number of individuals within the population.

Now let's look at it from the perspective of each alle at a given locus,

For the sake of discussion, let:

p = the frequency of allele A.

q = the frequency of allele a.

              therefore...

It is possible that the numbers of homozygous dominant and heterozygotes and homozygous recessives can change without changing the probability of finding individual alleles (p's and q's).

What about an example of how such equations can be used to calculate the frequencies of allele "A" and "a" within a population.

In essence, a population that is NOT changing genetically is said to be atHardy–Weinberg equilibrium; in that the allelic and genotypic frequencies within a population has reached this state and do not change from generation to generation.

To appreciate the importance of the HW equilibrium, Five essential assumptions about the population must be made.

 

 

IF the above conditions of the Hardy–Weinberg equilibrium are met, two consequences must follow.

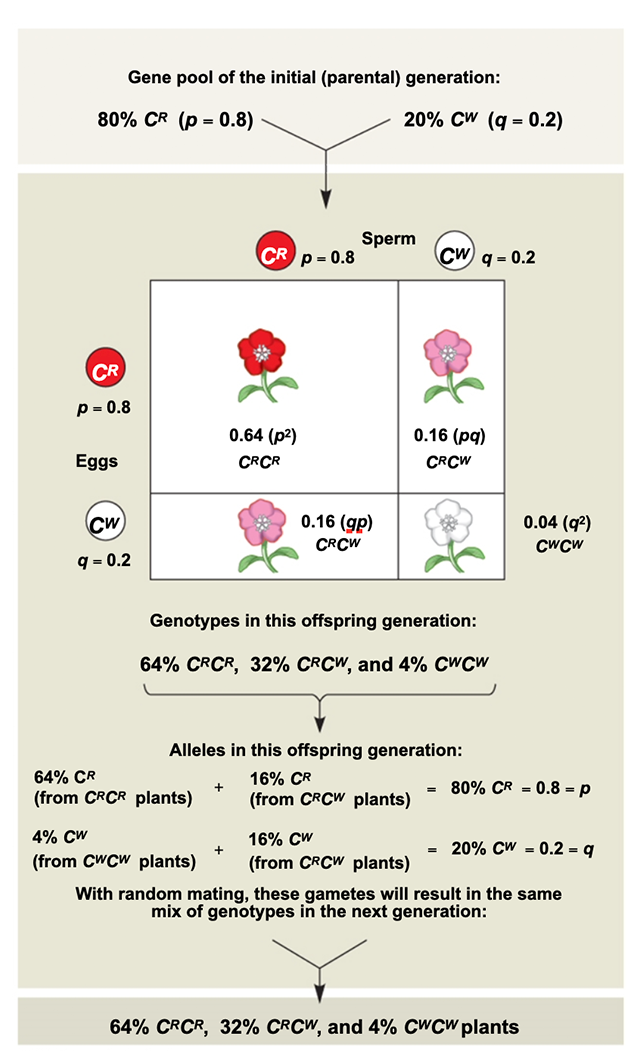
(a) The frequencies of alleles at a given locus will remain constant from generation to generation.

(b) After one generation of random mating, the genotypic frequencies will not change.

Restating the second result in the form of an equation that takes into account the allelic frequencies, produces the Hardy–Weinberg equation:

p²  +  2pq  +  q²  = 1

An example of the Hardy–Weinberg equation in use (see below), and how it is derived from Mendelian first principles can be seen below.

 

        

 

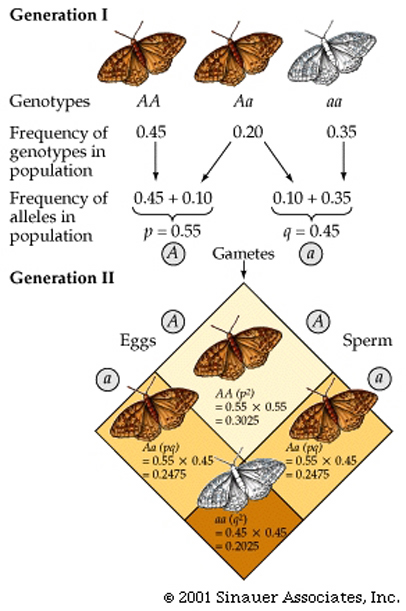
Note that this example also shows that there are two ways to produce a heterozygote, hence the overall probability for obtaining a heterozygote is "2pq", not just "pq".

So, why is this "Hardy–Weinberg equilibrium" so important?

Because it suggests that allelic frequencies remain the same from generation to generation unless some agent acts upon them to change them... and that something is EVOLUTION.

Thus, dominant alleles would not necessarily "dominate" the presence of the recessive allele unless either one had an effect upon any of the five criterea necessary to appreciate the HW equilibrium.

It also illustrates the distribution of genotypes that can be expected (for a given population) at "genetic equilibrium" for any value p or q (which can be determined empirically).

But the conditions for any maintenance of the equilibrium are far too stringent for any given natural population, so...

is it relevant to the real world?

Yes. It is the equivalent of a "null hypothesis" to the scientific method. ie it is the condition where "nothing happens".

As such, it allows scientists to determine (a) whether evolutionary agents are operating and (b) the identity of the agents that might be operating to change the pattern away from the equilibrium.... Erin Brokovitch story

Microevolution: Changes in the Genetic Structure of Populations

"Evolutionary agents" cause changes in the allelic and genotypic frequencies within a population.
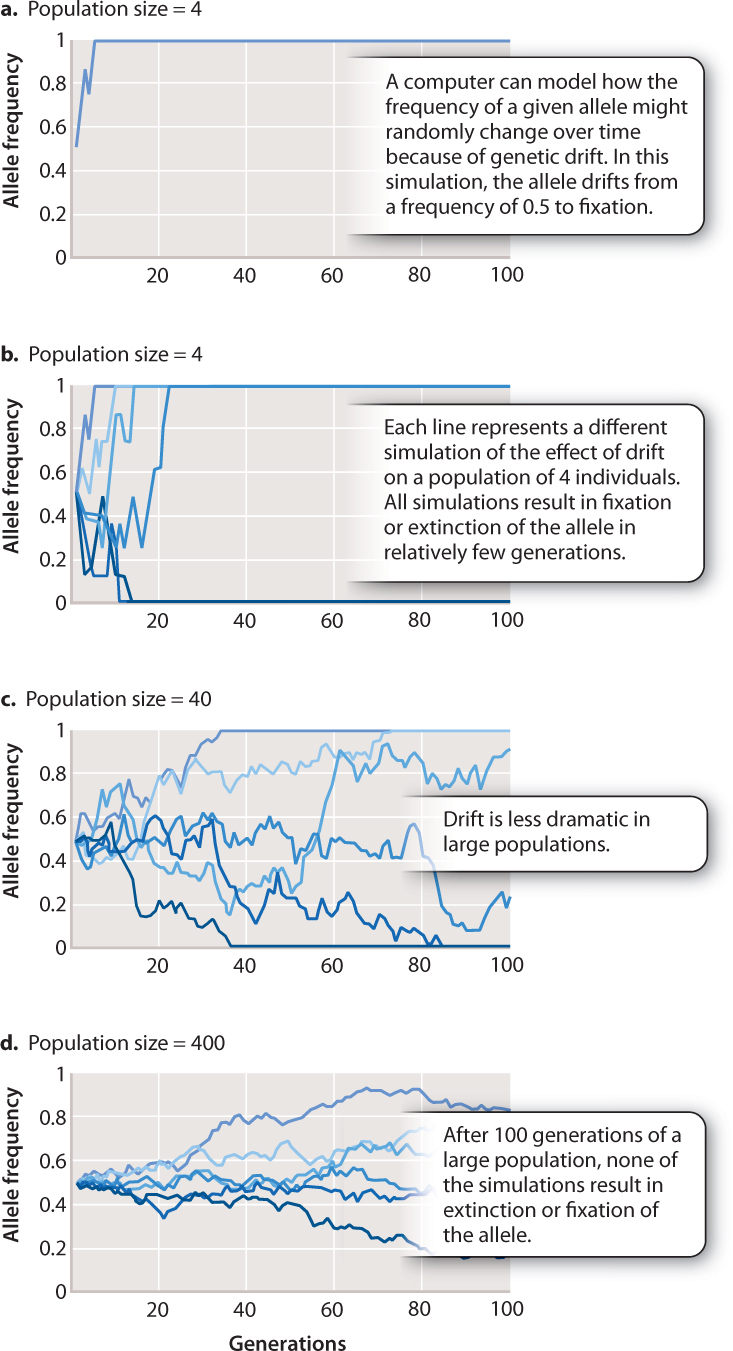
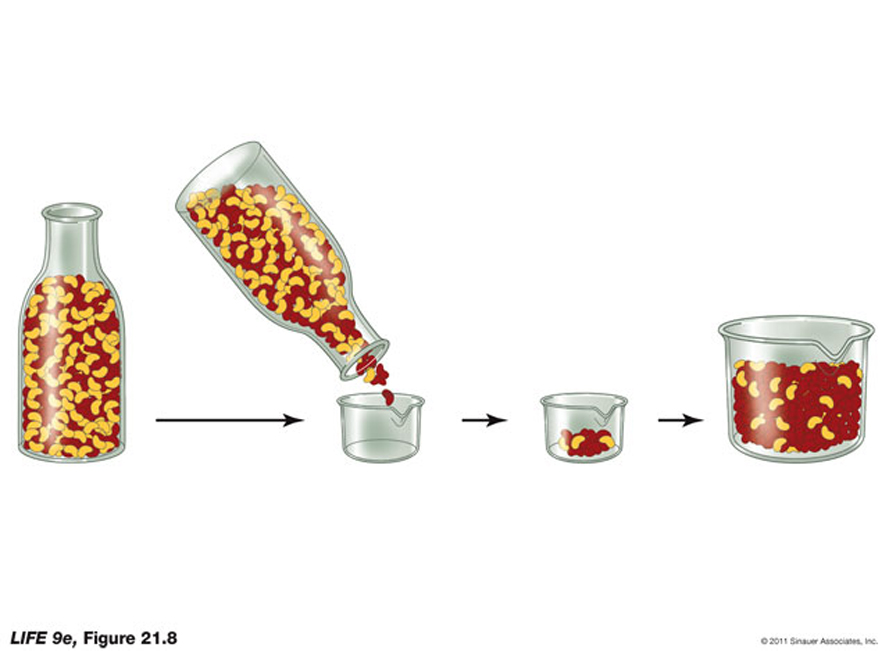
Since the changes in the gene pool of a population constitute small-scale evolutionary changes, they are referred to as microevolution.

We have discussed -to varying degrees- that some of the known evolutionary agents are gene flow, random genetic drift, non-random mating, and natural selection.

To a limited extent, we have also discussed, mutations, which are changes in the genetic material that can either be deleterious or beneficial to the function of an allele/gene, and which may or may not be selected for or against in a given population..

 

 

While most of these mutations appear to be random (e.g. copying errors, as the DNA is synthesized), and are normally either harmful or "neutral" (i.e. they do not affect their bearers ability to survive, and or procreate), some mutations are actually beneficial. Whatever the direct consequence they provide for a heterogenous population.

Indeed, the origin of all genetic variation is heterogeneity in the germ-line cells (why do we not care about somatic cell variations?)

Even though mutations are sufficient to create considerable genetic variation mutation rates, are relatively low; approximately one mutation per million loci is a typical frequency.

Thus, even though the very presence of mutations within a population means that one of the principle conditions that are necessary for the Hardy–Weinberg equlibrium to exist can never be met, the rate at which mutations arise at any particular locus is so low that the consequences of any neutral mutations would result in only very small deviations from Hardy–Weinberg expectations.

If large deviations are found within a population, then either the mutation is selective, or it would be appropriate to look for reasons why the mutation rate is so high -i.e. look for evidence of and additional agent that is causing the problem.

Such analyses have added important insights into how we can view evolutionary changes that have occurred over the ages, and have allowed us to appreciate that evolutionary rates can vary in two ways: slowly through "neutral" mutational changes to a gene pool and/or quite dramatically by some other changes in the assumptions that would normally hold for a gene pool in some form of equilibrium.

Hopefully helping to understand some of the different variables that have helped create evolutionary changes over evolutionary time and how the rates of change can differ for different types of living organisms. For example, it can detect potential "bottlenecks" in population development, as the ferquency of alleles, under this circumstance would be severely reduced.