- Home
Welcome !
Welcome to john houghton's home page for his biology courses. This site is designed as a hub for curating and sharing lectures, course syllabi, assignments, and links to relevant resources. Use the menu bar at the top of the screen to navigate through the site.
(Please note: this page is currently under construction.)

- BIOL 2107
Fall '23 CRN86772
Lectures: (1)
- Courses
BIOL 2107 Principles of Biology I
- Resources
General Resources
pdf download / video w/o sound
Electron Shells -Animation / Covalant Bond -Animation / Ionic Bond -Animation
Some of the important highlights of Chemistry -from a Biologist's perspective
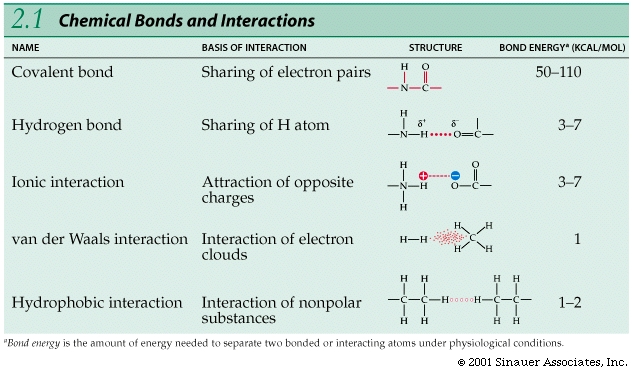
Bonds between atoms / ions vary in strength; the strongest bonds are covalent bonds, which involve sharing electrons.

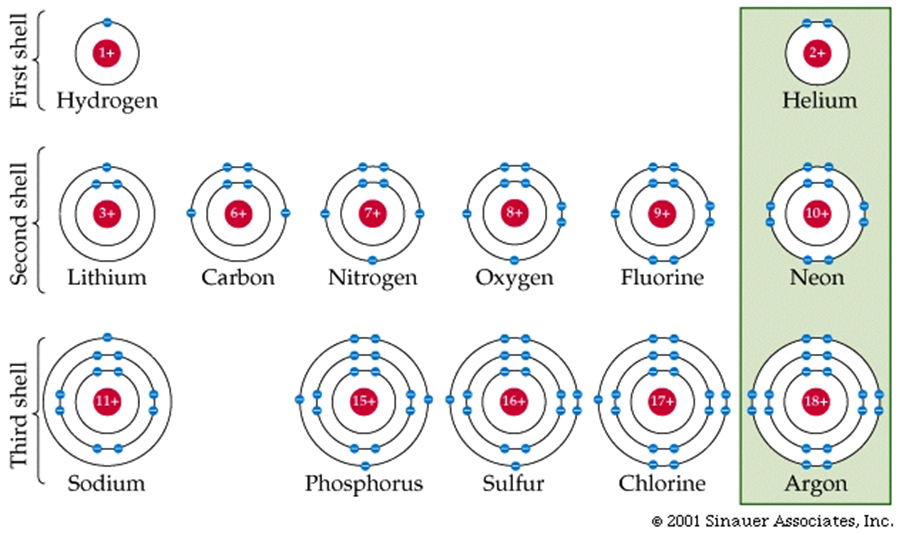
Electron shells and orbitals allow for bonds to be formed between and among different elements.
Unlike the sharing—or even the unequal sharing—that characterizes covalent bonds, ionic bonds involve a complete transfer of one or more electrons.
Covalent bonds consist of shared pairs of electrons
A covalent bond is the sharing of a pair of electrons between two atoms.
In hydrogen molecules, H2, a pair of electrons share a common orbital and spend equal amounts of time around each of the two nuclei.
Ions are formed when an atom completely loses or gains electrons.
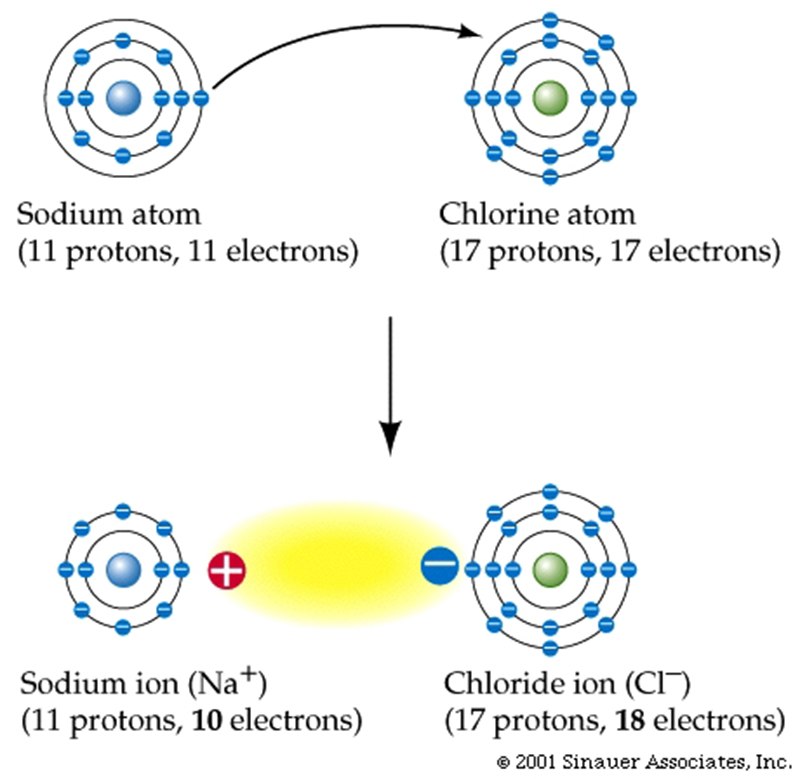
Ions are always symbolized by + or – superscripts, designating which ion has lost or gained an electron.
Positively charged ions are called cations: Na+ is an example.
Negatively charged ions are called anions: Cl– is an example.
Calcium ion Ca2+ is an example of an ion that has two more protons than electrons.
The Ca2+ ion is a cation and is said to be divalent.
The aluminium ion is Al3+.
Iron can be either Fe2+ (ferrous ion) or Fe3+ (ferric ion). In solution Fe2+ sometimes changes to Fe3+ and vice versa.
Cuprous ion is Cu+, and cupric ion is Cu2+.
Complex ions commonly occur in biological systems. These are groups of covalently bonded atoms that together carry an electrical charge. Examples are NH4+ (ammonium ion), SO42– (sulphate ion), and PO43– (phosphate ion).
Ionic bonds are formed by the attractions of opposite charges.
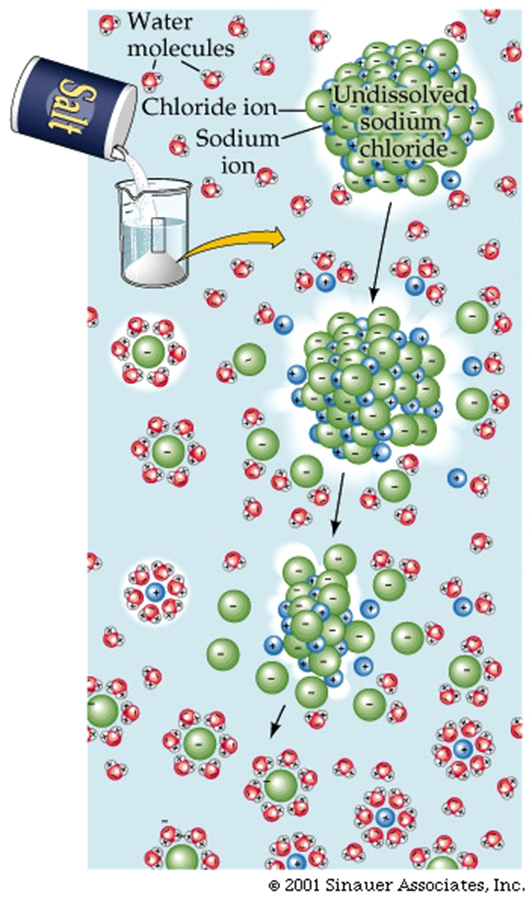
The most obvious form of a mixture of ions is Table salt, which has chloride and sodium ions, that are held together by opposite charge attractions.
These attractions are strong, but when introduced into water, the partial charges of the water molecules can easily interfere with the ionic bonds. For example, the figure below shows how water molecules cluster around cations and anions to "dissolve" table salt. This is one pf thereasons why water is SO IMPORTANT for LIFE to exist.
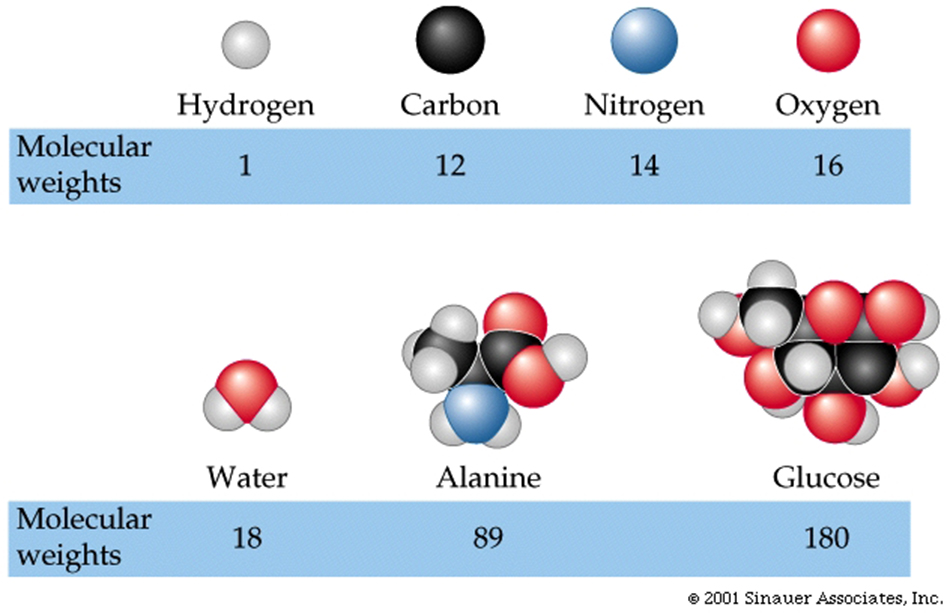
Molecular formula: a compound depicted by its chemical symbols
Molecular weight (or mass): the sum of all the atomic weights in a molecule.
The molecular weight of H2 is 2.
Mole: the amount of a substance in grams whose weight is equal to its molecular weight.
One mole of H2 weighs 2 g.
One mole of any given compound contains approximately 6.02 x 1023 molecules of that compound (Avogadro's number).
A 1 molar (1 M)solution is one mole of a compound dissolved (normally in water) to make one litre.
One mole of sodium chloride (table salt) is the atomic weight of sodium (23.0) plus the atomic weight of chlorine (35.5), or 58.5 (in grams). When 58.5 grams of sodium chloride are dissolved in some amount of water, and then additional water is added to create a final volume of a litre, the solution is said to be a 1 molar solution .
Acids, Bases, and the pH Scale
Acids donate H+; bases accept H+.
If a compound increases the H+ ion concentration when added to water, then the compound is acidic.
If the reaction is complete, such as HCl --> H+ + Cl–, it is a strong acid.
Not all acids "dissolve" fully into their ionic forms in water. Acetic acid, for instance, does not completely react and is therefore called a weak acid.
If a compound increases the OH– ion concentration when added to water, then the compound is basic. Just as with acids, there are strong and weak bases. Water is actually a very "weak" acid, and has a slight tendancy to ionize (break apart) into H+ and OH–.
This ionization is very important for living creatures and the chemical reactions they must perform.
A strong base completely reacts: NaOH ---> Na++ OH–.
A weak base, such as bicarbonate, does not completely react, and accepts H+ ions in several ways, one being the formation of weak carbonic acid.
Reversible chemical reactions-in principle- can proceed in either direction, but the extent of reversibility may vary.
—NH2 + H+ <---> —NH3+
A carboxyl group (—COOH) is common in a number of biological compounds.
As we will discuss further, carboxyl groups also function as both an acid and as a base, because —COOH <--> —COO– + H+.
pH is the measure of hydrogen ion concentration, and was first introduced In 1909, Soren Sorensen, a Danish biochemist, who proposed what is now known as the pH scale. Sorensen developed a simple equation to express the hydronium ion concentrations logarithmically. The pH of a solution is -1 times the logarithm (of the base 10) of the hydronium ion concentration (expressed in moles per liter). The equation for the pH of a solution is: pH = - log[H3O+]
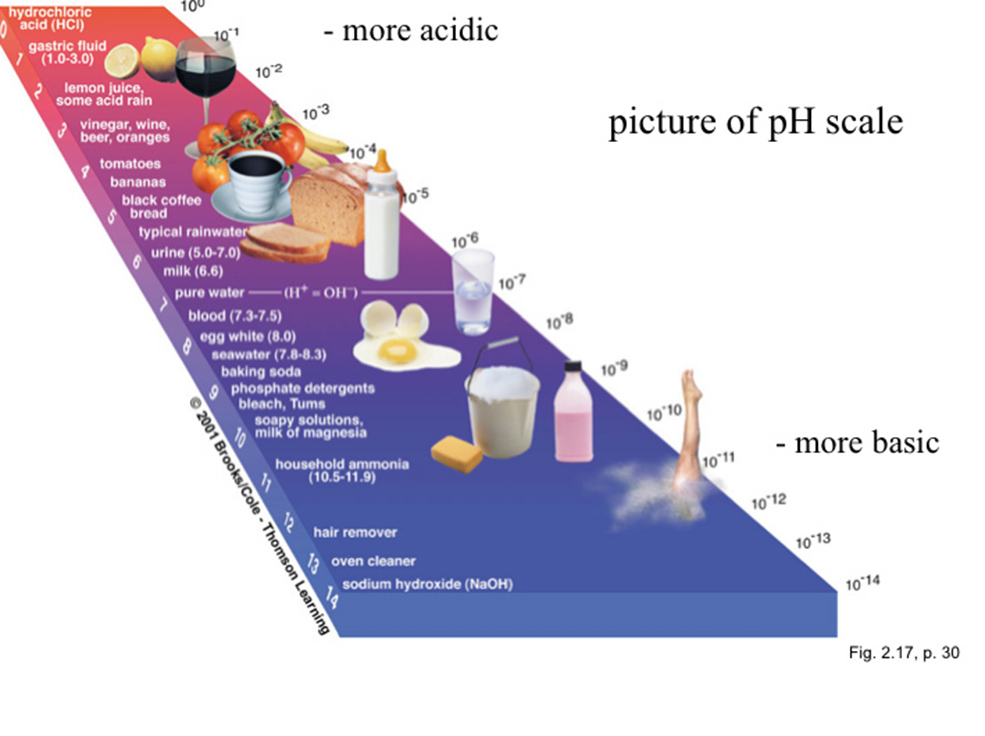
The pH scale indicates the strength of a solution of an acid or base. The scale is arrayed as a set of values 1 through 14. These values may be measured by electronic instruments.
The pH value is defined as the negative logarithm of the hydrogen ion concentration in moles per liter (molar concentration).
A pH 7 means that the concentration of hydrogen ions (or more specifically the concentration of hydro(xo)nium ions (which are simply H+ attached to a water molecule) is [1 x 10–7].
Even strongly acidic solutions have mostly water molecules and not ions.
A solution with pH 1 has one H+ for every 556 water molecules
A solution at pH 1 can have a powerfully corrosive effect on a variety of materials including metals, polysaccharides, proteins, nucleic acids, and bone.
Buffers minimize pH change
A Buffer is a mixture of a weak acid and its corresponding base.
Because buffers can react with both added bases and acids, they make the overall solution more resistant to changes in.
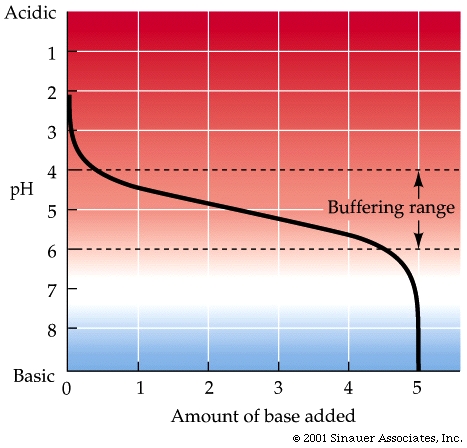
Different buffers transition to and from ionic forms at their particular characteristic pH ranges.
Buffers are common in biology and extremely important in the regulation of the internal environments of organisms.
Many important biological buffers transition around pH 7, which keeps the pH near neutral.
Buffers illustrate the law of mass action: The addition of components to one side of a reaction drives the reaction in the direction that uses that component. As an acid or a base is added to a solution, the buffer will change form, transitioning between ionic and non-ionic bonds
The Properties of Molecules
Molecules range in size and molecular weight from the very smallest, H2, to the relatively massive, such as the DNA molecule that makes up the length of a chromosome and contains millions of atoms.
Carbon-containing molecules are called "organic molecules", most of which contain hydrogen and oxygen, and many contain nitrogen and phosphorus. Nitrogen, oxygen, and carbon are also all found in the air.... and can even be found on Mars

 <
<
Hydrogen and oxygen are found in water.
All molecules have three-dimensional shapes. CH4 is tetrahedral.
Properties of Water ... (H2O) somewhat unique...
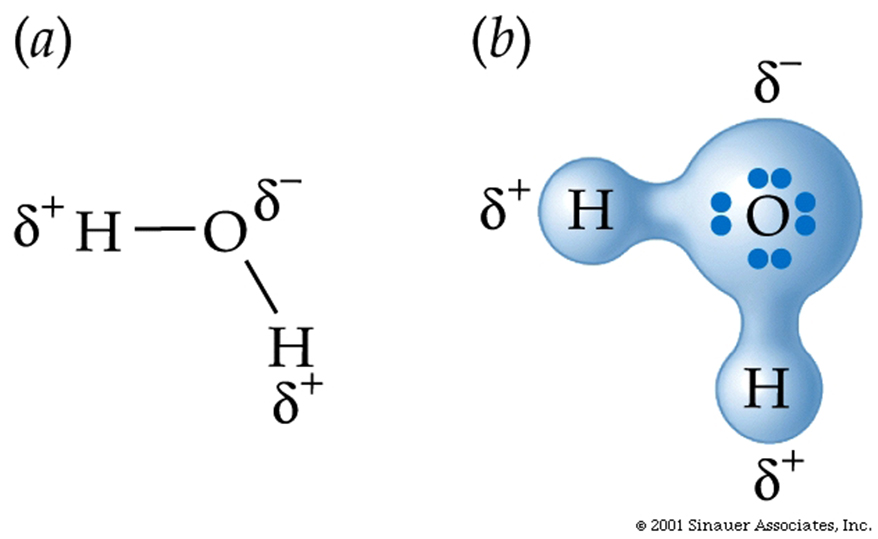
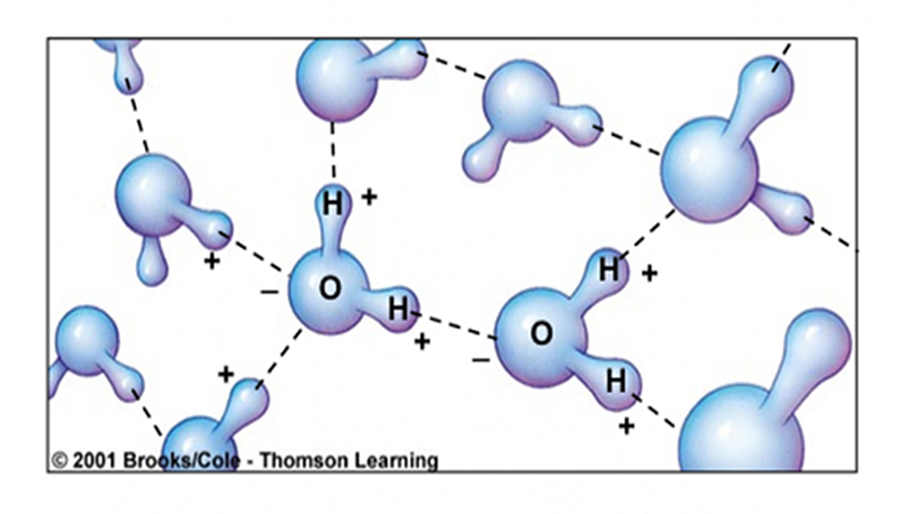
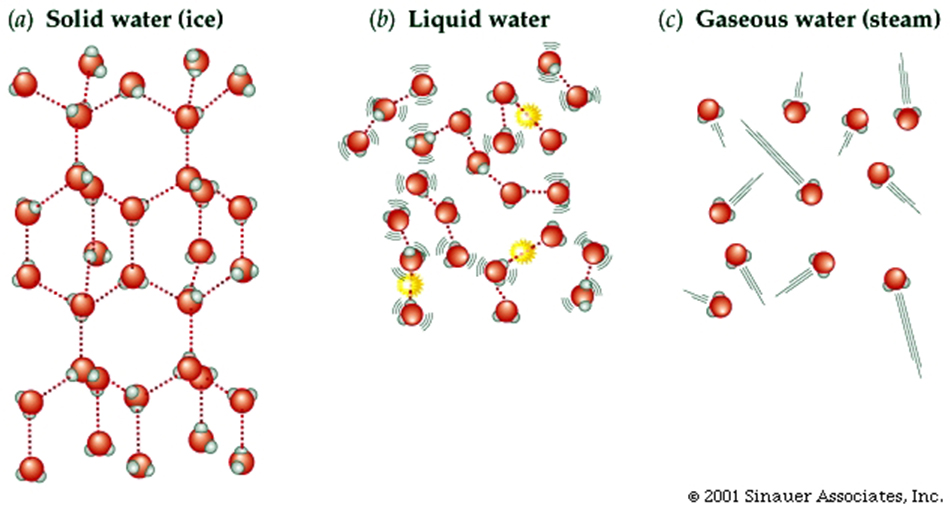
Larger molecules have potentially more complex shapes that are the result of a combination of the atoms present and the ways they are linked together.
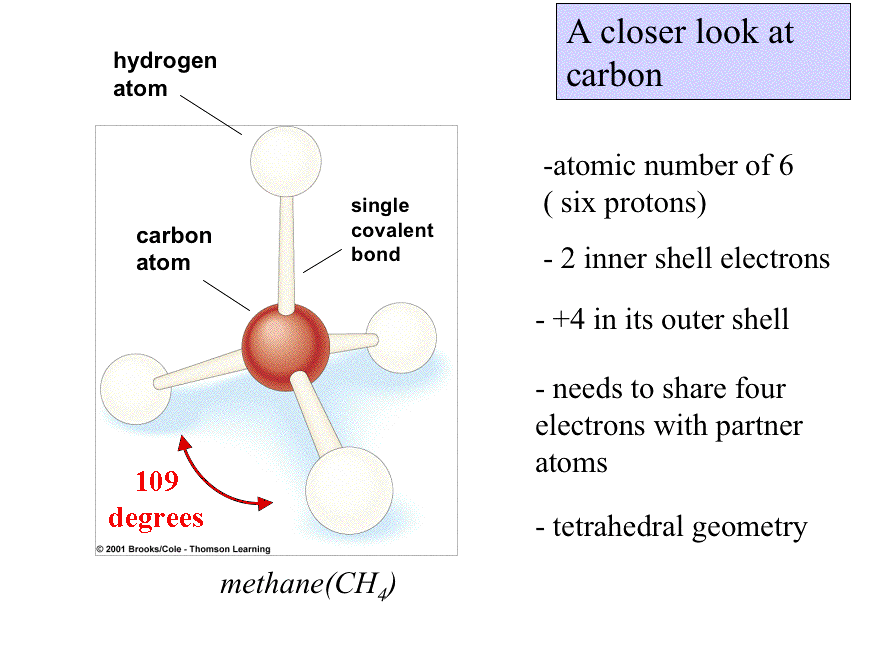
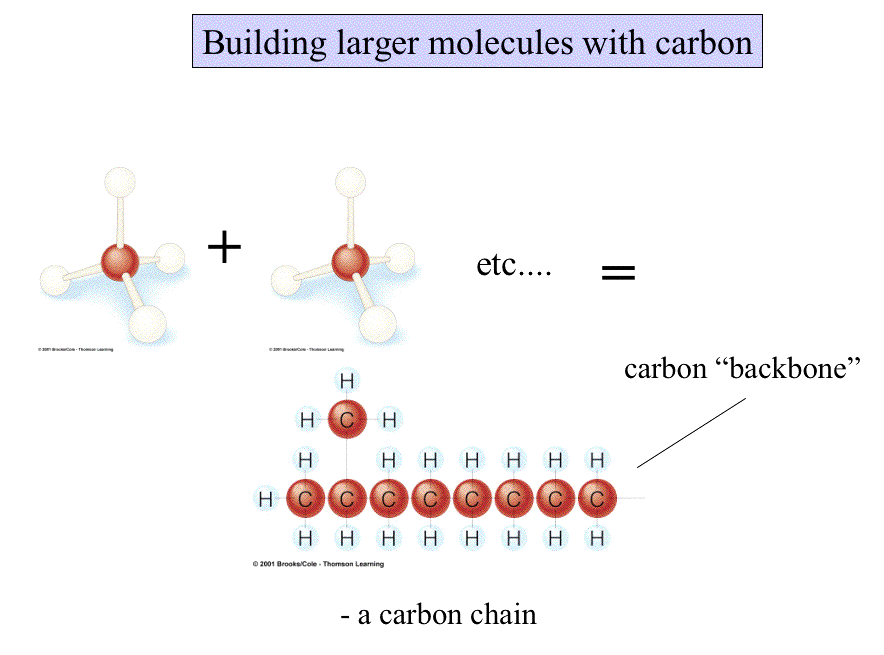
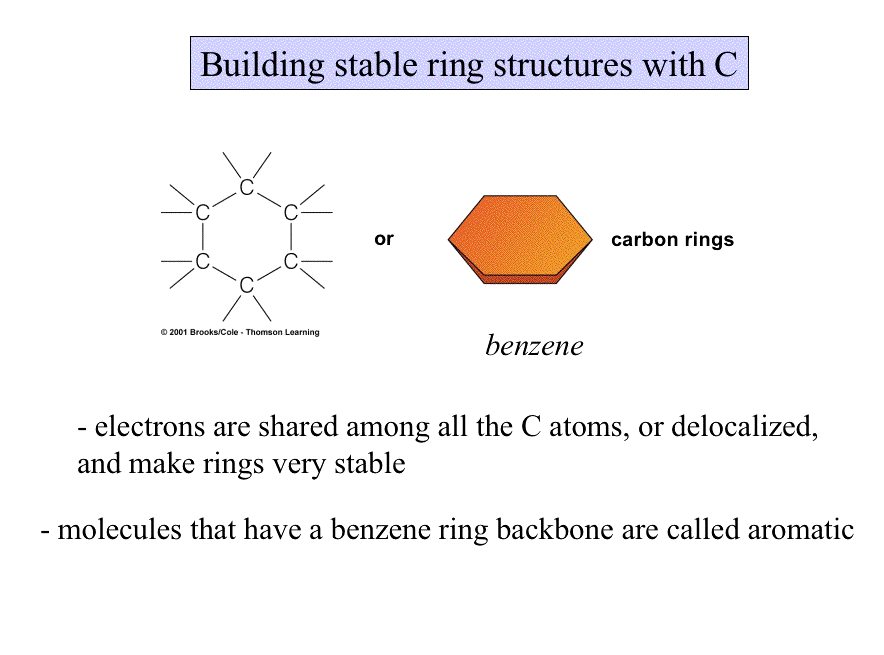
Some molecules are long and rope-like; some are ball-shaped; any which way, shape influences the behavior and function of molecules.
Indeed, Chemists use the characteristics of composition, structure, reactivity, and solubility to help classify molecules.
Macromolecules: Giant Polymers
There are four major types of biological macromolecules: proteins, carbohydrates, lipids (?), and nucleic acids.
These macromolecules are made the same way in all living things, and they are present in all organisms in roughly the same proportions.
Macromolecules are essentially giant polymers, which are formed by covalent linkages of smaller units called monomers.
Molecules with molecular weights greater than 1,000 Daltons (atomic mass units) are usually classified as "macromolecules".
Some of the many roles of macromolecules include:
Energy source
Energy storage
Structural support
Catalysis
Transport
Protection and defense
Regulation of metabolic activities
Maintenance of homeostasis
Means for movement, growth, and development
Heredity
The diverse functions of macromolecules are invariably related to their shape and the chemical properties of their monomers.

About Contact GSU Academics Degrees & Majors |
Admissions Undergraduate Research Dept. of Biology |
Libraries University Library Campus Life Housing |
Athletics Alumni
|

|


